All of the graphs are graphed with an asymptote, they are all graphed when a point touches the x-axis. Asymptote are also based on sine and cosine. When they are graphed, sine and cosine continuously go up and down, the other four trig functions have an asymptote and continue but at some point only half of it is graphed and then a period is graphed and it repeats. The only graphs that change direction are tangent and contingent. Tangent is graphed as positive while cotangent is graphed as negative.
Tangent
The ratio for tangent is sine/cosine and an asymptote only exists for tangent when cosine equals zero.
Tangent's period is at pi and its parent asymptotes are at pi/2 and 3pi/2.
 |
| (http://www.regentsprep.org/Regents/math/algtrig/ATT7/otherg91.gif) |
The ratio for cotangent is cosine/sine and the the asymptote only exists when sine is equal to zero. The parent asymptotes are 0 and pi; the reason why it is zero is because sine is equal to y on the unit circle and in this case sine (y/r) equals zero. this means that sine is equal to any value on the unit circle where y equals zero.
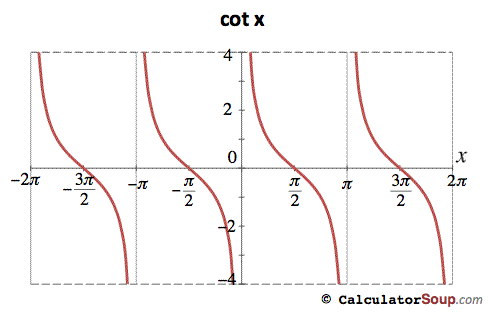 |
| (http://www.calculatorsoup.com/images/trig_plots/graph_cot_pi.gif) |
Secant is the reciprocal of 1/cosine and an asymptote only exists when cosine is zero. when graphing secant there should be a parabola in the middle of one period. it is graphed from the middle point of the cosine graph that is graphed first.
 |
| (http://www.calculatorsoup.com/images/trig_plots/graph_sec_pi.gif) |
the reciprocal of cosecant is 1/sine and when sine equals zero cosecant is 1/0 which means that there is an asymptote because it is undefined. when cosecant is graphed there should be two parabolas in one period in between the asymptotes but they should be graphed from the lowest and highest points in the period.
 |
| (http://www.calculatorsoup.com/images/trig_plots/graph_csc_pi.gif) |
No comments:
Post a Comment