BQ#4: Unit T Concept 3

Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill?
If we think back to the unit circle we can remember that tangent is positive in quadrant one, negative in quadrant two, positive in quadrant three, and negative in quadrant four. we should also remember that the ratio for tangent is sine/cosine or y/x. we should keep in mind that the asymptotes for tangent are where x, cosine, equals zero and that the asymptotes are at pi/2 and 3pi/2. an easy way to remember which direction tangent is graphed is that it is graphed according to which quadrants it is positive and negative in. cotangent

(http://hotmath.com/hotmath_help/topics/graphing-tangent-function/tan-graph.gif)

cotangent has asymptotes at zero, pi, and 2pi because sine is equal to zero and those three points are where cotangent is undefined. they are both positive above the x-axis and they are both negative below the x-axis but the reason for why cotangent's asymptotes go downhill is because the asymptotes and boundaries determine which direction the graph will go.

(http://www.mathipedia.com/GraphingSecant,Cosecant,andCotangent_files/image033.jpg)

BQ#3: Unit T Concepts 1-3

How do graphs of sine and cosine relate to each of the others?
  All of the graphs are graphed with an asymptote, they are all graphed when a point touches the x-axis. Asymptote are also based on sine and cosine. When they are graphed, sine and cosine continuously go up and down, the other four trig functions have an asymptote and continue but at some point only half of it is graphed and then a period is graphed and it repeats. The only graphs that change direction are tangent and contingent. Tangent is graphed as positive while cotangent is graphed as negative.


Tangent
The ratio for tangent is sine/cosine and an asymptote only exists for tangent when cosine equals zero.
Tangent's period is at pi and its parent asymptotes are at pi/2 and 3pi/2.

(http://www.regentsprep.org/Regents/math/algtrig/ATT7/otherg91.gif)

Cotangent

The ratio for cotangent is cosine/sine and the the asymptote only exists when sine is equal to zero. The parent asymptotes are 0 and pi; the reason why it is zero is because sine is equal to y on the unit circle and in this case sine (y/r) equals zero. this means that sine is equal to any value on the unit circle where y equals zero. 

(http://www.calculatorsoup.com/images/trig_plots/graph_cot_pi.gif)

Secant

Secant is the reciprocal of 1/cosine and an asymptote only exists when cosine is zero. when graphing secant there should be a parabola in the middle of one period. it is graphed from the middle point of the cosine graph that is graphed first. 

(http://www.calculatorsoup.com/images/trig_plots/graph_sec_pi.gif)

Cosecant

the reciprocal of cosecant is 1/sine and when sine equals zero cosecant is 1/0 which means that there is an asymptote because it is undefined. when cosecant is graphed there should be two parabolas in one period in between the asymptotes but they should be graphed from the lowest and highest points in the period. 

(http://www.calculatorsoup.com/images/trig_plots/graph_csc_pi.gif)

BQ#5: Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do?

 The ratio for sine is y/r and the ratio for cosine is x/r. We know that in order for there to be an asymptote that the value has to be zero, or undefined. We also know that r equals 1 so sine is y/1 and cosine is x/1. The value of r is not zero, so we do not end up with an asymptote. The other four trig functions have asymptotes because their x or y value in the denominator is not 0, it can vary depending on the values of x and y.

(http://ramanujan.math.trinity.edu/rdaileda/teach/m1312f08/invtrig/7.jpg)

(http://www.analyzemath.com/trigonometry/graph_cosecant.gif)

(http://www.mathipedia.com/GraphingSecant,Cosecant,andCotangent_files/image033.jpg)

(http://www.mathamazement.com/images/Pre-Calculus/04_Trigonometric-Functions/04_06_Graphs-of-Other-Trig-Functions/secant-graph.JPG)

BQ#2: Unit T Concept Intro

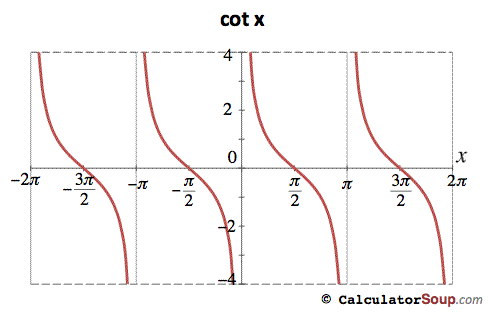
1. How do the trig graphs relate to the Unit Circle?
Trig graphs relate to the unit circle because of ASTC. Whether the quadrant is positive or negative all depends on whether it is sine, cosine, tangent, or cotangent. An example would be if it is sine, then the first quadrant would be positive, the first quadrant is always positive, the second quadrant would be positive because that's the quadrant where sine is positive, and the third and fourth quadrants would be negative.

http://www.analyzemath.com/trigonometry/graph_sine.gif

Period
The period of sine and cosine is 2pi because that is how many units on the x-axis they cover while going through one cycle. The period of cotangent and tangent is pi because they cover pi units on the x-axis while going through one cycle.

Amplitude
sine and cosine have restrictions that they can only be between 1 and -1. One and negative one are also the lowest and highest points when being graphed. Cosecant, tangent, cotangent, and secant do not have an amplitude.

Reflection #1: Unit Q: Verifying Trig Identities

1. Verifying a trig function means to get one side of the problem to equal the other. Think of it as proofs from Geometry. It's related to it because identities are being used to get the final answer. When you are verifying a trig function you should know what your identities are or else you're going to have a bad time.
2. The most helpful tip was that you can't divide a trig function by another trig function and that when in doubt, square the function. Squaring the function is a lot more work because of the extraneous solutions but it's better than staring at the paper wondering what to do next. The most important tip is to memorize all of the identities so it'll make verifying it a lot easier.
3. When I am given a trig function to verify I first look at the identities to see what I am going to use. I also check if I am going to have to multiply to get the least common denominator or when I have to move something over to the other side to make the function equal 0. When i have a function that is squared I take out the GCF and I usually end up with a Pythagorean Identity. If I'm stuck, I square the functions to see if I can go somewhere with that.